SECURE HASH ALGORITHM - SHA 512

Hashing Algorithm — SHA-512

So, SHA-512 does its work in a few stages. These stages go as follows:

1. Input formatting
2. Hash buffer initialization
3. Message Processing
4. Output

Let’s look at these one-by-one.

1. Input Formatting:

SHA-512 can’t actually hash a message input of any size, i.e. it has an input size limit. This limit is imposed by its very structure as you may see further on. The entire formatted mesage has basically three parts: the original message, padding bits, size of original message. And this should all have a combined size of a whole multiple of 1024 bits. This is because the formatted message will be processed as blocks of 1024 bits each, so each bock should have 1024 bits to work with.

<pic: original message>

Original message

Padding bits

The input message is taken and some padding bits are appended to it in order to get it to the desired length. The bits that are used for padding are simply ‘0’ bits with a leading ‘1’ (100000…000). Also, according to the algorithm, padding needs to be done, even if it is by one bit. So a single padding bit would only be a ‘1’.

The total size should be equal to 128 bits short of a multiple of 1024 since the goal is to have the formatted message size as a multiple of 1024 bits (N x 1024).

<pic: msg + pad>

Message with padding

Padding size

After this, the size of the original message given to the algorithm is appended. This size value needs to be represented in 128 bits and is the only reason that the SHA-512 has a limitation for its input message.

Since the size of the original message needs to be represented in 128 bits, the message size can be at most (2¹²⁹-1) bits and also taking into consideration the necessary single padding bit, it maximum size would then be (2¹²⁹-2). Even though this limit exists, it doesn’t actually cause a problem since the actual limit is so high (2¹²⁹-2 = 680,564,733,841,876,926,926,749,214,863,536,422,910 bits).

<pic: msg + pad +size>

Message with padding and size

Now that the padding bits and the size of the message have been appended, we are left with the completely formatted input for the SHA-512 algorithm.

Formatted Message

2. Hash buffer initialization:

The algorithm works in a way where it processes each block of 1024 bits from the message using the result from the previous block. Now, this poses a problem for the first 1024 bit block which can’t use the result from any previous processing. This problem can be solved by using a default value to be used for the first block in order to start off the process. (Have a look at the second-last diagram).

Since each intermediate result needs to be used in processing the next block, it needs to be stored somewhere for later use. This would be done by the hash buffer, this would also then hold the final hash digest of the entire processing phase of SHA-512 as the last of these ‘intermediate’ results.

So, the default values used for starting off the chain processing of each 1024 bit block are also stored into the hash buffer at the start of processing. The actual value used is of little consequence, but for those interested, the values used are obtained by taking the first 64 bits of the fractional parts of the square roots of the first 8 prime numbers (2,3,5,7,11,13,17,19). These values are called the Initial Vectors (IV).

Why 8 prime numbers instead of 9? Because the hash buffer actually consists of 8 subparts (registers) for storing them.

<pic: IV>

Hash buffer and Initialization Vector values

3. Message Processing:

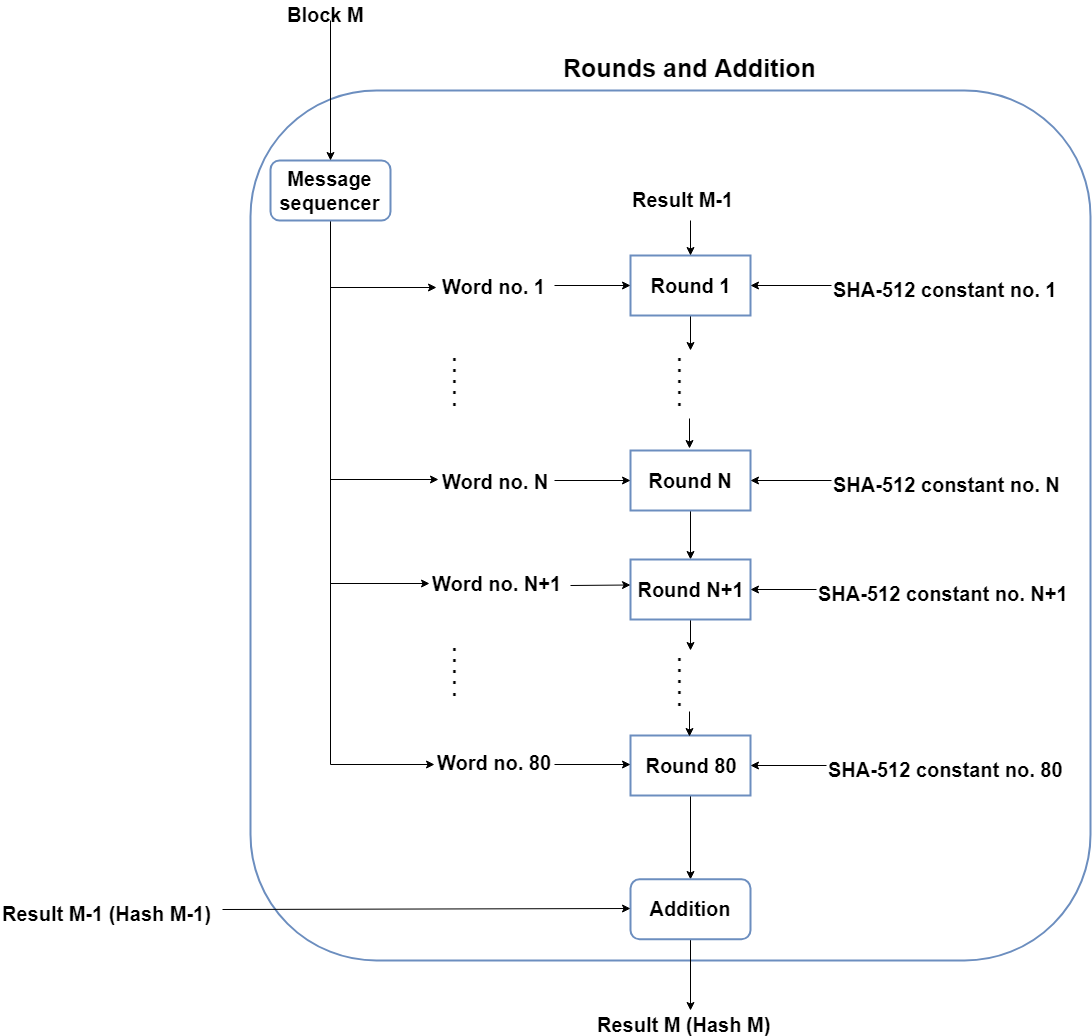
Message processing is done upon the formatted input by taking one block of 1024 bits at a time. The actual processing takes place by using two things: The 1024 bit block, and the result from the previous processing.

This part of the SHA-512 algorithm consists of several ‘Rounds’ and an addition operation.

<pic: Formatted input 1024 bit blocks;F(M.n ,H.n-1)=H.n>

William Stallings, Cryptography and Network Security — Principles and Practise (Seventh Edition) referred for diagram

So, the Message block (1024 bit) is expanded out into ‘Words’ using a ‘message sequencer’. Eighty Words to be precise, each of them having a size of 64 bits.

Rounds

The main part of the message processing phase may be considered to be the Rounds. Each round takes 3 things: one Word, the output of the previous Round, and a SHA-512 constant. The first Round doesn’t have a previous Round whose output it can use, so it uses the final output from the previous message processing phase for the previous block of 1024 bits. For the first Round of the first block (1024 bits) of the formatted input, the Initial Vector (IV) is used.

SHA-512 constants are predetermined values, each of whom is used for each Round in the message processing phase. Again, these aren’t very important, but for those interested, they are the first 64 bits from the fractional part of the cube roots of the first 80 prime numbers.Why 80? Because there are 80 Rounds and each of them needs one of these constants.

Once the Round function takes these 3 things, it processes them and gives an output of 512 bits. This is repeated for 80 Rounds. After the 80th Round, its output is simply added to the result of the previous message processing phase to get the final result for this iteration of message processing.

4. Output:

After every block of 1024 bits goes through the message processing phase, i.e. the last iteration of the phase, we get the final 512 bit Hash value of our original message. So, the intermediate results are all used from each block for processing the next block. And when the final 1024 bit block has finished being processed, we have with us the final result of the SHA-512 algorithm for our original message.

Thus, we obtain the final hash value from our original message. The SHA-512 is part of a group of hashing algorithms that are very similar in how they work, called SHA-2. Algorithms such as SHA-256 and SHA-384 are a part of this group alongside SHA-512. SHA-256 is also used in the Bitcoin blockchain as the designated hash function.