RSA cryptosystem

RSA is an asymmetric system , which means that a key pair will be generated (we will see how soon) , a public key and a private key , obviously you keep your private key secure and pass around the public one.

The algorithm was published in the 70’s by Ron Rivest, Adi Shamir, and Leonard Adleman, hence RSA , and it sort of implement’s a trapdoor function such as Diffie’s one.

RSA is rather slow so it’s hardly used to encrypt data , more frequently it is used to encrypt and pass around symmetric keys which can actually deal with encryption at a faster speed.

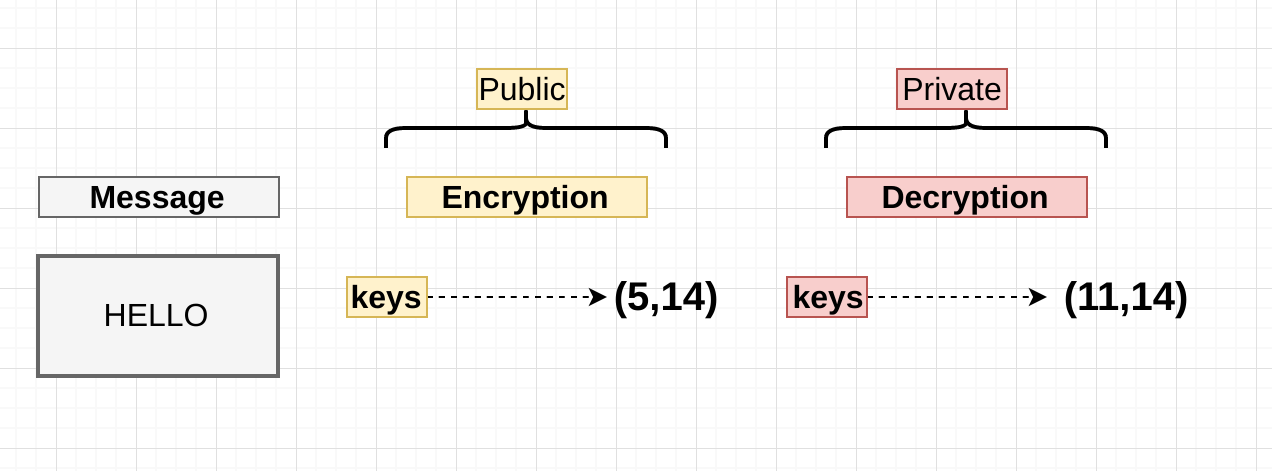
We’ve got a message (“HELLO”) , and we’ve picked two tuples with two numbers each ( I will explain how these came about later). Obviously there’s no arithmetic operation we can perform with strings , so the message has to be convert it to something , so let’s say “HELLO” converts using some conversion algo to “2”

Normally , in production , a lot of different techniques are used to encode the message and padding is also used

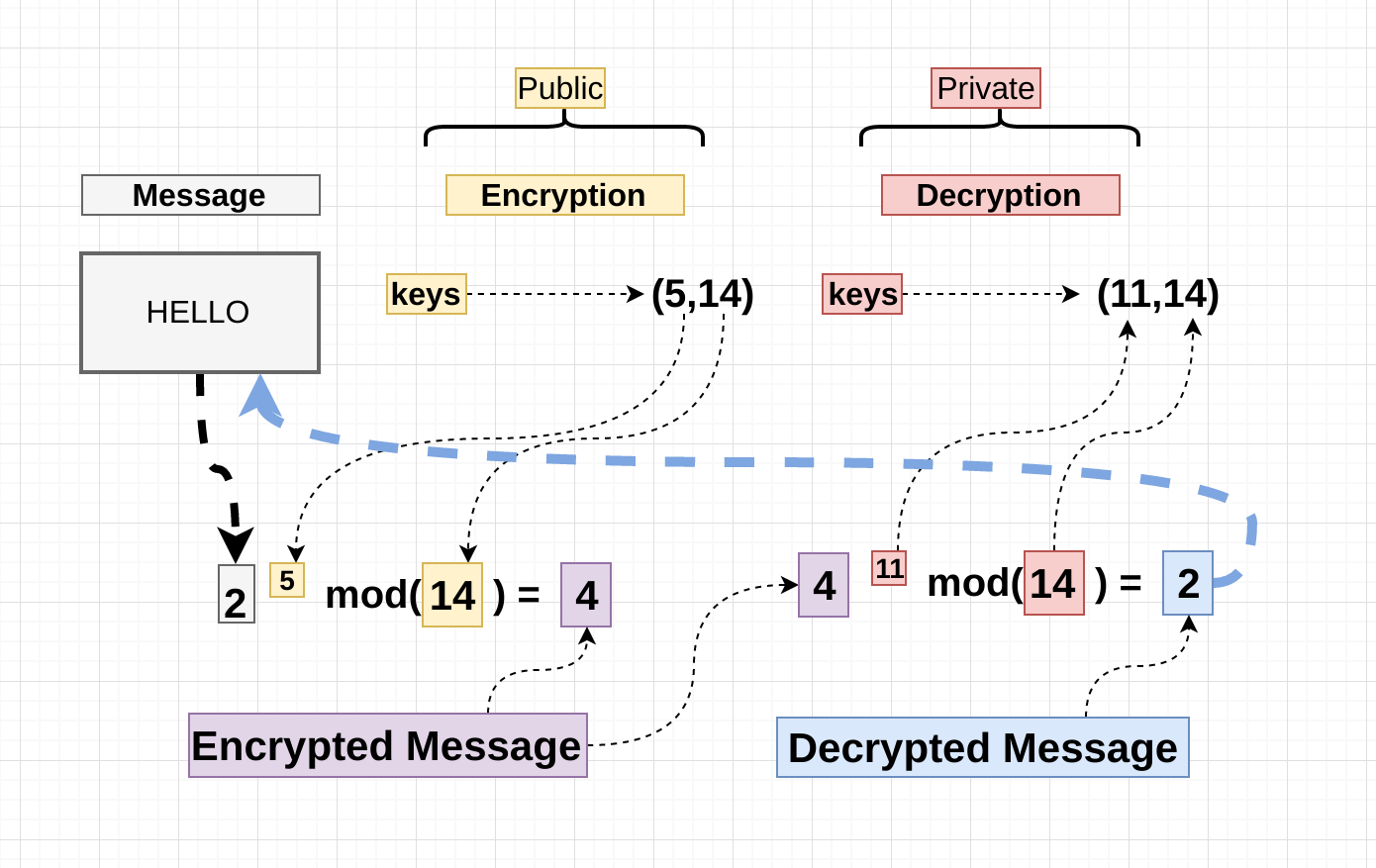
The interesting bit is how we come about those numbers , and how (5,14) is related to (11,14), and this is the interesting part i believe , let’s start:

The details of the Decryption/Encryption pair:

1. Pick two prime numbers , I will pick 2 and 7 , lets call them p and q

P = 2 and Q = 7

2. Multiply P and Q , and that becomes the modulus

N = P * Q = 14

3. Make a list between 1 and 14 and remove the common factors:

Now there’s an easy way to get this and that is:

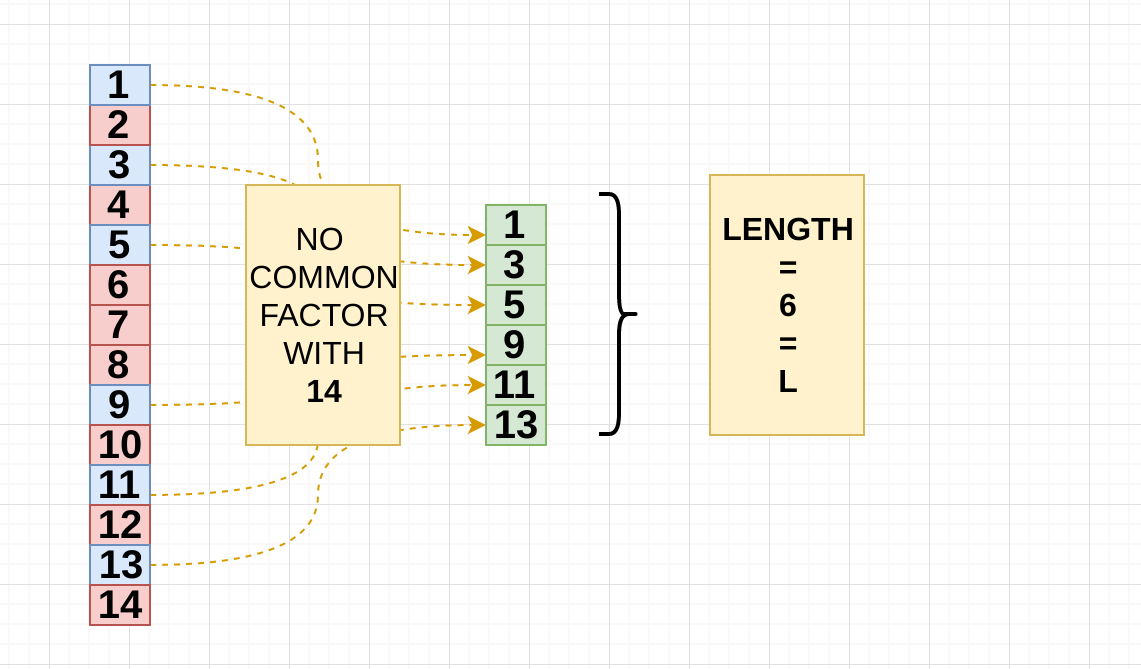
( Q - 1 ) * ( P - 1) = L

(7 - 1 ) * ( 2 -1 ) = 6

Great let’s save this number , let’s call it “L”

4. Now we get to pick the encryption key , in the example was (5,14) , we know 14 is the modulus.

So for the encryption key there’s a few rules:

• it’s got to be between 1 and L

[2,3,4,5]

• Coprime with L (6) and the Modulus (14) , the answer is 5 , there’s no other possibility .

So there we came to a conclusion of why we picked (5,14)

5. The Decryption part , In the example we’ve picked (11,14) , again 14 is the modulus but where does 11 come from?? , from now on let’s call it D , let’s find out why D is 11:

D has to follow one rule and this is it:

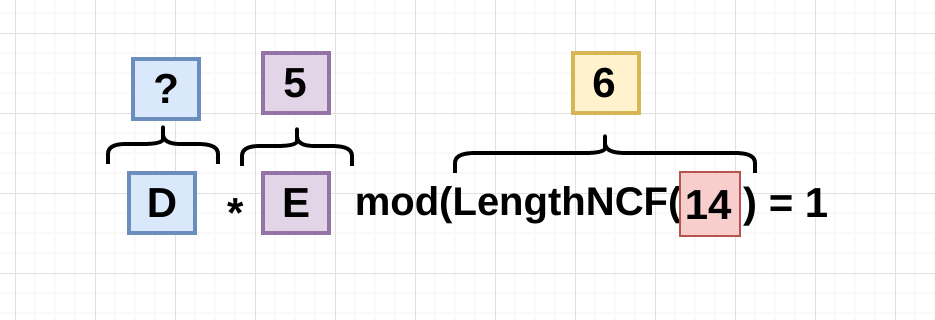
So the Decryptor(11) multiplied by the Encryptor(5) modulus the length of the non coMmon factor with the modulus(14) has to be equals to 1.

D * E % LNCF(N) = 1

11 * 5 % 6 = 1

So we know if we multiply D * E and E is 5 , D will need to be a common factor of 5 , so:

So I’ve made a list of numbers from 1 to 50 and , filtered the ones that when multiplied by E and moduled by LNCF(N) are equals 1 , so let’s see if those can decrypt the message :) , Remember the encrypted message is “4”,and the decrypted message is “2” so the function should be something like:

4 ** D % 14 = 2 <---Decrypted message

So let’s do a little list comprehension to see if the rule works:

Great ! it worked , you see how applying the function to all the Decryption keys that follow the rule (D * E % LNCF(N) = 1) , decrypted the message successfully .